Pengertian Sistem Bilangan Dan Konversi Bilangan
Februari 22, 2019
Pengertian sistem Bilangan Dan Konversi Bilangan - Kebanyakan orang mengerti bila mengatakan bahwa kita mempunyai 9 poin emas. Angka 9 merupakan bagian dari sistem bilangan desimal yang kita gunakan setiap hari. Tetapi peralatan elektronika kita menggunakan suatu sistem bilangan "Asing" yang disebut Binner. Komputer digital dan sistem yang berdasarkan microprocessor menggunakan sistem angka asing lain yang Hexadecimal. Setiap orang yang bekerja dibidang elektronika harus mengetahui bagaimana mengubah bilangan - bilangan dari sistem bilangan desimal ke binner dan dari binner ke bilangan desimal yang sering dipakai. Anda akan dapat juga mengubah sistem bilangan binner kebilangan hexadecimal. Serta sistem bilangan desimal ke hexadecimal. Sistem komputer yang lain menggunakan sistem bilangan oktal anda akan mempelajari membuat conversi bilangan binner, oktal, dan hexadecimal.
Berikut ini uraian pembahasan tentang sistem bilangan dan konversi bilangan yang kami berikan pada materi ini :
A. Sistem Bilangan Decimal
Sebelum mempelajari dengan bilangan binner, ada baiknya mengetahui tentang system bilangan yang umum dipakai, yaitu ( desimal, bilangan, basic 10 ).
Berikut ini uraian pembahasan tentang sistem bilangan dan konversi bilangan yang kami berikan pada materi ini :
A. Sistem Bilangan Decimal
Sebelum mempelajari dengan bilangan binner, ada baiknya mengetahui tentang system bilangan yang umum dipakai, yaitu ( desimal, bilangan, basic 10 ).
Untuk menghitung suatu bilangan desimal, dari nilai yang terkecil ( yang paling kanan ). Pada basis 10, maka kalikan nilai paling kanan dengan 100 dan ditambah dengan nilai di kiri yang dikalikan dengan 101, Dst.
Untuk bilangan yang dibelakang "Koma", bilangan digunakan 101, 102, Dst.
- Contoh : 1, 2, 4, 3 = ( 1x103 ) + ( 2x102) + ( 4x101 ) + ( 3x100 ) = 1000 + 200 + 40 + 3 = 1243.
Sistem bilangan desimal yang mempunyai komponen 0 sampai 9
- Contoh : Bilangan desimal " 7392 " mewakili suatu persamaan penjumlahan dari : ( 7 ribuan + 3 ratusan + 9 puluhan + 2 satuan ).
Ribuan, ratusan, puluhan dan satuan merupakan pemangkatan dari 10 yang menunjukkan posisi dari koefisien - koefisien : " 7392 " = ( 7x103 ) + ( 3x102 ) + ( 9x101 ) + ( 2x100).
➤ Secara umum = a3. a2, a1, a0, a-1, a-2, a-3.
➤ Atau dioperasikan sebagai berikut :
= ( a3.103 ) + ( a2.102 ) + ( a1.101 ) + ( a0.100 ) + ( a-1.10-1 ) + ( a-2.10-2 ) + ( a-3.10-3 )
⇓
( a3.R3 ) + ( a2.R2 ) + ( a1.R1 ) + ( a0.R0 ) + ( a-1.R-1 ) + ( a-2.R-2 ) + ( a-3.R-3 ) ..... N.
B. Sistem Bilangan Basis Bilangan
Maka : ( 410 ) = ( a5, a4, a3, a2, a1, a0 )2 = ( 101001 )2.
➜ Sisa 1 = 1
Sisa 0 = 0
➜ Konversikan bilangan desimal 41 ke bil.biner ( bil.berbasis 2 ) menggunakan sistem sisa.
Untuk bilangan yang dibelakang "Koma", bilangan digunakan 101, 102, Dst.
- Contoh : 1, 2, 4, 3 = ( 1x103 ) + ( 2x102) + ( 4x101 ) + ( 3x100 ) = 1000 + 200 + 40 + 3 = 1243.
Sistem bilangan desimal yang mempunyai komponen 0 sampai 9
- Contoh : Bilangan desimal " 7392 " mewakili suatu persamaan penjumlahan dari : ( 7 ribuan + 3 ratusan + 9 puluhan + 2 satuan ).
Ribuan, ratusan, puluhan dan satuan merupakan pemangkatan dari 10 yang menunjukkan posisi dari koefisien - koefisien : " 7392 " = ( 7x103 ) + ( 3x102 ) + ( 9x101 ) + ( 2x100).
➤ Secara umum = a3. a2, a1, a0, a-1, a-2, a-3.
➤ Atau dioperasikan sebagai berikut :
= ( a3.103 ) + ( a2.102 ) + ( a1.101 ) + ( a0.100 ) + ( a-1.10-1 ) + ( a-2.10-2 ) + ( a-3.10-3 )
⇓
( a3.R3 ) + ( a2.R2 ) + ( a1.R1 ) + ( a0.R0 ) + ( a-1.R-1 ) + ( a-2.R-2 ) + ( a-3.R-3 ) ..... N.
B. Sistem Bilangan Basis Bilangan
Definisi :
1. Bil. Biner : Bilangan dasar yang dipakai untuk memanipulasi data pada hardware.
2. Bil. Oktal : Bilangan ini dipakai pada sipemograman untuk komputer generasi awal.
3. Bil. Desimal : Bilangan yang setiap hari kita pakai.
4. Bil. Hexadecimal : Bilangan yang dipakai untuk memanipulasi data pada software operasi microprocessor saat ini.
C. Konversi Bilangan Desimal Ke Bilangan Lain
➜ Sisa 1 = 1
Sisa 0 = 0
➜ Konversikan bilangan desimal 41 ke bil.biner ( bil.berbasis 2 ) menggunakan sistem sisa.
D. Bilangan Hexadecimal
Bilangan heksadesimal biasa disebut bilangan basis 16, artinya ada 16 simbol yang mewakili bilangan ini.
# Tabel berikut menunjukkan konversi bilangan hexadecimal.
Untuk konversi bilangan biner ke hexadecimal, perhatikan contoh berikut :
= ( 10110 1010 1001 0010 2 ).
= 0001 0110 1010 1001 0010
➜16A92.
Jadi, Bilangan biner : 10110101010010010 = 16A92. Penulisan bilangan hexadecimal biasa juga ditambahkan dengan karakter "ox" didepannya. Nilai 254316 sama nilainya dengan 0x2543.
E. Bilangan Oktal
Bilangan oktal disebut bilangan basis 8, artinya ada 8 simbol yang mewakili bilangan ini.
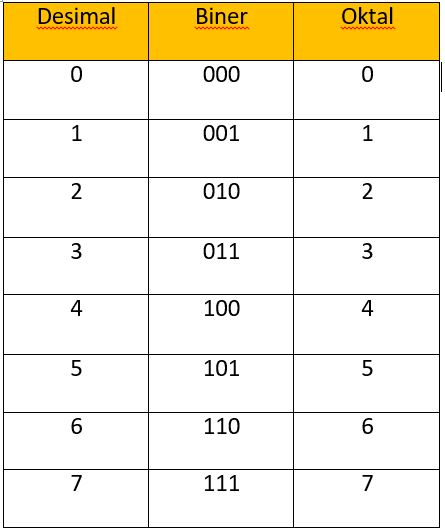
# Tabel berikut menunjukkan konversi bilangan oktal.
Untuk konversi bilangan biner ke oktal, perhatikan contoh berikut :
➜ 101101010100100102 = 010 110 101 010 010 010 = 2652228.
Jadi, Bil. biner 10110101010010010 sama dengan bilangan ( Oktal 265222 ).
F. Sandi Biner
Sandi biner BCD adalah Sandi yang mengkonversi bilangan desimal langsung kebilangan binernya. sehingga jumlah sandi BCD/10, sesuai dengan jumlah simbol pada desimal.
# Perhatikan contoh berikut :
- Contoh : 197 Sandi BCDnya adalah : 0001 1001 0111.
Sandi 2421 hampir sama dengan 8421, terutama untuk bilangan desimal 0 sampai 4 tetapi sandi berikutnya merupakan pencerminan yang dinversi.
# Perhatikan tabel berikut :
Seperti itu pembahasan mengenai pengertian dari Sistem Bilangan Dan Konversi Bilangan, Jika kalian ( Pembaca ) ada yang kurang paham / mempunyai pendapat yang berbeda dalam mengenai pemahaman dari pengertian dari Pengertian sistem Bilangan Dan Konversi Bilangan, Silahkan masukkan komentar dibawah ini mengenai pengertian diatas. "Hatur Nuhun".
E. Bilangan Oktal
Bilangan oktal disebut bilangan basis 8, artinya ada 8 simbol yang mewakili bilangan ini.
# Tabel berikut menunjukkan konversi bilangan oktal.
➜ 101101010100100102 = 010 110 101 010 010 010 = 2652228.
Jadi, Bil. biner 10110101010010010 sama dengan bilangan ( Oktal 265222 ).
F. Sandi Biner
Sandi biner BCD adalah Sandi yang mengkonversi bilangan desimal langsung kebilangan binernya. sehingga jumlah sandi BCD/10, sesuai dengan jumlah simbol pada desimal.
# Perhatikan contoh berikut :
Sandi 2421 hampir sama dengan 8421, terutama untuk bilangan desimal 0 sampai 4 tetapi sandi berikutnya merupakan pencerminan yang dinversi.
# Perhatikan tabel berikut :
Perhatikan sandi desimal S. sandi tersebut merupakan cermin dari sandi 4 desimal, tetapi logikanya diinversi begitu pula pada sandi desimal 6 yang merupakan cermin dari sandi desimal 3 yang diinversi dsb.
- Contoh : 37810 Sandi 2421nya adalah : 0011 1101 1110.
Baca Juga :
➜ ASCII singkatan dari " American Standart Code For Informasi Interchange ". standart yang digunakan pada industri untuk mengkodekan huruf, angka, dan karakter - karakter lain pada tabel ASCII dibagi menjadi 3 seksi :
a.) Kode system tak tercetak ( Non Printable System Codes ) antara 0 - 31
b.) ASCII lebih rendah ( Lower ASCII ), antara 32-137. Diambil dari kode sebelum ASCII digunakan. yaitu sistem american ADP, sistem yang bekerja pada 7 bit biner.
c.) ASCII lebih tinggi ( Higher ASCII ), antara 128-255 Bag. ini dari dapat diprogram, sehingga dapat mengubah karakter.